Kjernefysikk er den delen av fysikken som dreier seg om atomenes struktur og reaksjoner mellom atomkjerner. Innholdet i Einsteins energilikning, \(E=mc^2\) er helt avgjørende for å forstå kjernefysiske prosesser, ettersom alle av dem handler om energi-massekonverteringer.
Det er sammensetningen av nukleoner i en kjerne som avgjør om den er stabil eller ikke, typisk vil en kjerne med mange flere nøytroner enn protoner bli ustabil. En ustabil kjerne ønsker å nå en stabil tilstand – noe den gjør ved å sende ut radioaktiv stråling. Slike ustabile kjerner betegner vi som radioaktive.
Små kjerner kan fusjonere til én litt større kjerne, mens store kjerner kan fisjonere til to eller flere litt mindre kjerner. Begge disse to kjernefysiske reaksjonene, henholdsvis fusjon og fisjon, vil gi et massesvinn. Massen som angivelig “forsvinner” konverteres til energi, jf. Einsteins energilikning, \(E=mc^2\) . Energien som frigjøres vil altså tilsvare massesvinnet multiplisert med lysfarten opphøyd i andre. Selv om massen som blir til overs i reaksjonen er forsvinnende liten, vil energien som frigjøres bli vesentlig større. Det faktum at en liten masse kan konverteres til store mengder energi utnyttes i kjernekraftverk for å høste energi.
I 1905 utledet Albert Einstein den berømte likningen \(E=mc^2\). I denne likningen står \(E\) for hvileenergien, \(m\) for massen, og \(c\) for lysfarten. Det vi tydelig ser av denne likningen er at det er en helt klar sammenheng mellom energi og masse. Einstein beviste også matematisk at masse kan konverteres til energi, og at energi kan konverteres til masse. Denne nære sammenhengen mellom energi og masse danner selve grunnlaget for radioaktive prosesser, og kjernefysiske reaksjoner.

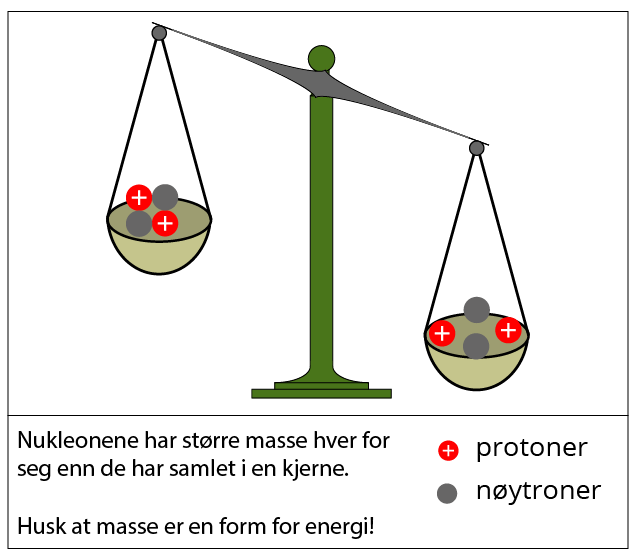
Massen til en atomkjerne er alltid litt mindre enn massen til nukleonene som utgjør kjernen lagt sammen. For eksempel vil to nøytroner og to protoner til sammen veie mer enn en vanlig heliumkjerne. Dette kan virke rart – det virker jo nesten som om masse har forsvunnet! Den massen som tilsynelatende er til overs, kaller vi massedefekten. Selv om det kan virke slik, forsvinner den ikke – den konverteres til energi. Denne energimengden er det som står for bindingsenergien i kjernen, og sørger for å holde nukleonene sammen. Ifølge Einsteins energilikning, vil denne bindingsenergien tilsvare massedefekten multiplisert med lysfarten opphøyd i andre.
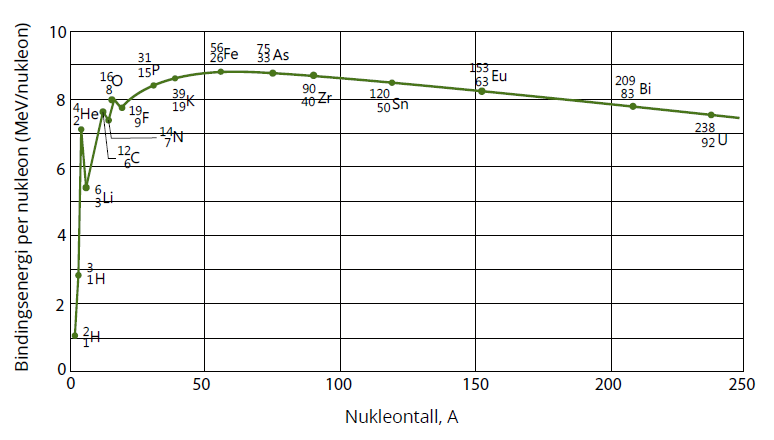
Grafen viser oss at bindingsenergien per nukleonNukleoner er kjernepartikler, altså de partiklene vi finner i kjernen i et atom. Dette innbefatter protoner og nøytroner. avtar i takt med økende atomnummer etter jern. De største kjernene vil derfor holdes dårligere sammen enn de små, noe som fører til at nukleonene kommer lenger fra hverandre. Nukleonene holdes sammen av den sterke kjernekraftenDenne kraften er en av de fire fundamentale kreftene i naturen, og den virker mellom nukleoner og elementærpartikler. Det er denne kraften som holder nukleonene i en kjerne sammen., men bare på veldig korte avstander. Denne kraften er grunnen til at protonene i kjernen ikke frastøter hverandre slik som like poler på magneter. Men, den sterke kjernekraftenDenne kraften er en av de fire fundamentale kreftene i naturen, og den virker mellom nukleoner og elementærpartikler. Det er denne kraften som holder nukleonene i en kjerne sammen. virker bare på svært korte avstander, og når størrelsen på atomkjernen øker, vil det bli vanskelig for den sterke kjernekraftenDenne kraften er en av de fire fundamentale kreftene i naturen, og den virker mellom nukleoner og elementærpartikler. Det er denne kraften som holder nukleonene i en kjerne sammen. å holde nukleonene sammen. Det kan nemlig bli vanskelig å unngå at den elektromagnetiske kraftenDen elektromagnetiske kraften holder atomer og molekyler sammen. Den virker tiltrekkende mellom ulike ladninger, men frastøtende mellom like ladninger. virker mellom protonene og støter dem fra hverandre. For kjernene er det energimessig fordelaktig å ha omtrent like mange protoner som nøytroner. Kjerner med atomnummer høyere enn 30 har likevel behov for flere nøytroner enn protoner for å hindre protonene å frastøte hverandre. Derfor vil ikke antall nøytroner og protoner være likt til enhver tid. Dette fører til at atomkjernen blir ustabil, og kan spontant sende ut en partikkel, eller dele seg (fisjon) for å prøve å nå en stabil tilstand. Denne labiliteten gir opphav til det vi kaller radioaktiv stråling, og nuklider som sender ut radioaktiv stråling kaller vi radioaktive stoffer.

Radioaktive prosesser
Radioaktive stoffer vil sende ut radioaktiv stråling. Det er tre forskjellige slike radioaktive prosesser:
Alfa-stråling: utsendelse av en heliumkjerne
\(^{241}_{\,\,95} \text{Am} \enspace \to \enspace ^{237}_{\,\,93}\text{Np} + ^{4}_{2}\text{He}\)
Beta-stråling: utsendelse av et elektron og et anti-elektronnøytrino. Her blir et nøytron omdannet til et proton og et elektron. I tillegg sendes alltid et anti-elektronnøytrino ut.
\( {^{1}_{0}\text{ n}} \enspace \to \enspace {^{1}_{1}\text{ p}} + {^{\,\,0}_{-1}\text{ e}} + {\overline{v}_e} \)
Gamma-stråling: Etter en kjerne har sendt ut en alfa- eller beta-partikkel kan kjernen være i eksitert tilstandEn partikkel som er i eksitert tilstand er blitt tilført energi. Økningen i energi betegnes ut ifra et referansepunkt, ofte grunntilstanden til atomet. Atomet trives ikke i denne eksiterte tilstanden, og søker mot grunntilstanden. Når en partikkel de-eksiterer vil den overflødige energien frigis i form av fotoner.. Her vil den imidlertid ikke befinne seg lenge, fordi den alltid vil søke seg ned mot grunntilstanden. Da vil den eksiterte kjernen kvitte seg med den overflødige energien ved å sende ut(emittereÅ emittere betyr å sende ut, som for eksempel stråling.) et foton med svært høy energi, en gammapartikkel.
\( {^{14}_{\,\,6}\text{C}} \enspace \to \enspace {^{14}_{\,\,7}\text{N}^{*}} + {^{\,\,0}_{-1}e} + {\overline{v}_e} \)
\({^{14}_{\,\,7}\text{N}^{*}} \enspace \to \enspace {^{14}_{\,\,7}\text{N}} + \gamma \)
Fusjon og Fisjon

Figur 3 viser i bunn og grunn de samme variasjonene for nuklideneEn nuklide er en bestemt sammensetning av nukleoner. som figur 2. Istedenfor å vise bindingsenergien per nukleonNukleoner er kjernepartikler, altså de partiklene vi finner i kjernen i et atom. Dette innbefatter protoner og nøytroner. som en funksjon av nukleontallet, viser denne grafen imidlertid massen per nukleonNukleoner er kjernepartikler, altså de partiklene vi finner i kjernen i et atom. Dette innbefatter protoner og nøytroner. som en funksjon av nukleontallet. Følgelig vil disse grafene se påfallende like ut, ettersom massedefekten som utgjør bindingsenergien kommer til uttrykk i begge fremstillingene.
Denne figuren egner seg godt til å forklare hvorfor fusjoner og fisjoner kan gi en reaksjonsenergi.
I fusjonen mellom hydrogenisotopeneIsotoper av et grunnstoff er atomer med likt antall protoner i kjernen, men forskjellig antall nøytroner i kjernen. For eksempel er protium, deuterium og tritium tre isotoper av hydrogen, med henholdsvis 0,1 og 2 nøytroner i tillegg til det ene protonet som gjør atomet til hydrogen. deuteriumEn isotop av hydrogen. Det er stabilt, dvs. ikke radioaktivt. Har et proton og et nøytron i kjernen. og tritiumEn isotop av hydrogen. Det er ustabilt, dvs. radioaktivt. Har et proton og to nøytron i kjernen., vil vi få dannet en heliumkjerne og et nøytron:
\({^{2}_{1}\text{H}} + {^{3}_{1}\text{H}} \enspace \to \enspace {^{4}_{2}\text{He}} + {^{1}_{0}\text{n}}\)
Dersom vi summerer massen til produktene, og deretter trekker dette fra summen av massen til reaktantene, vil det være intuitivt å tenke at differansen blir lik 0. Dette stemmer dog ikke – her får vi et massesvinn. Massen som tilsynelatende “forsvinner”, konverteres til energi i henhold til Einsteins likning – på samme måte som at massedefekten konverteres til bindingsenergi. Det samme kan vi se ut i fra grafen i figur 3.
Når et nøytron sendes mot Uran-235, vil vi få Uran-236 – en særdeles ustabil nuklide som raskt vil fisjonere. Man kan betrakte det siste nøytronet som absorberes som dråpen som får begeret til å renne over. Summen av massen til produktene er også her lavere enn summen av massen til reaktantene – vi har et massesvinn.
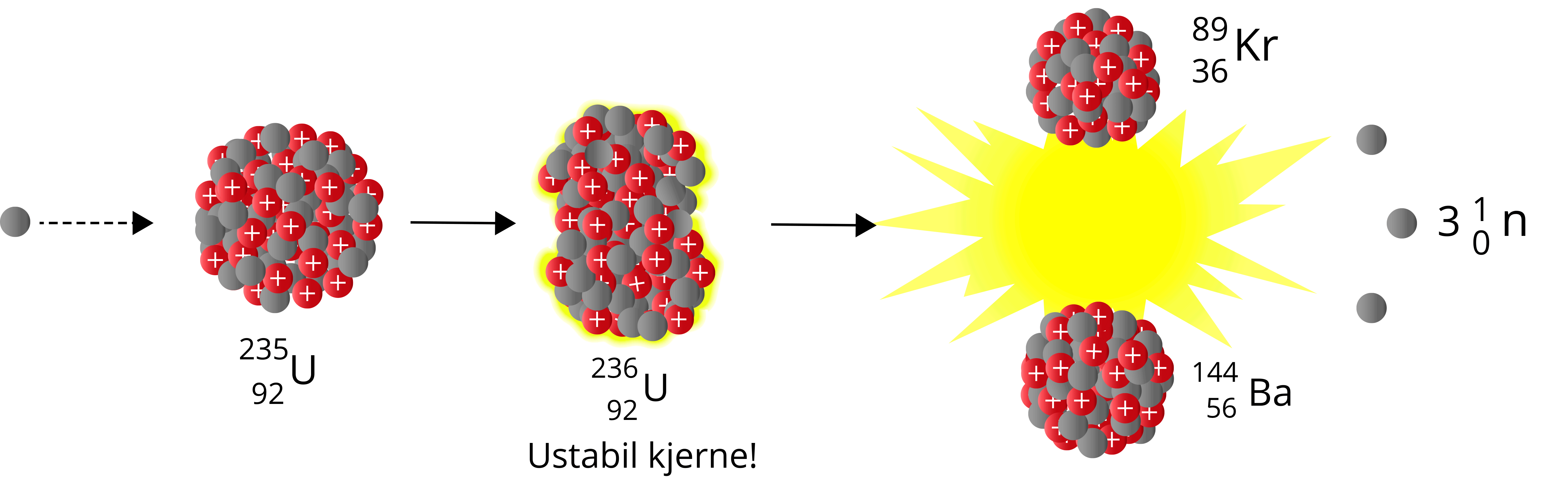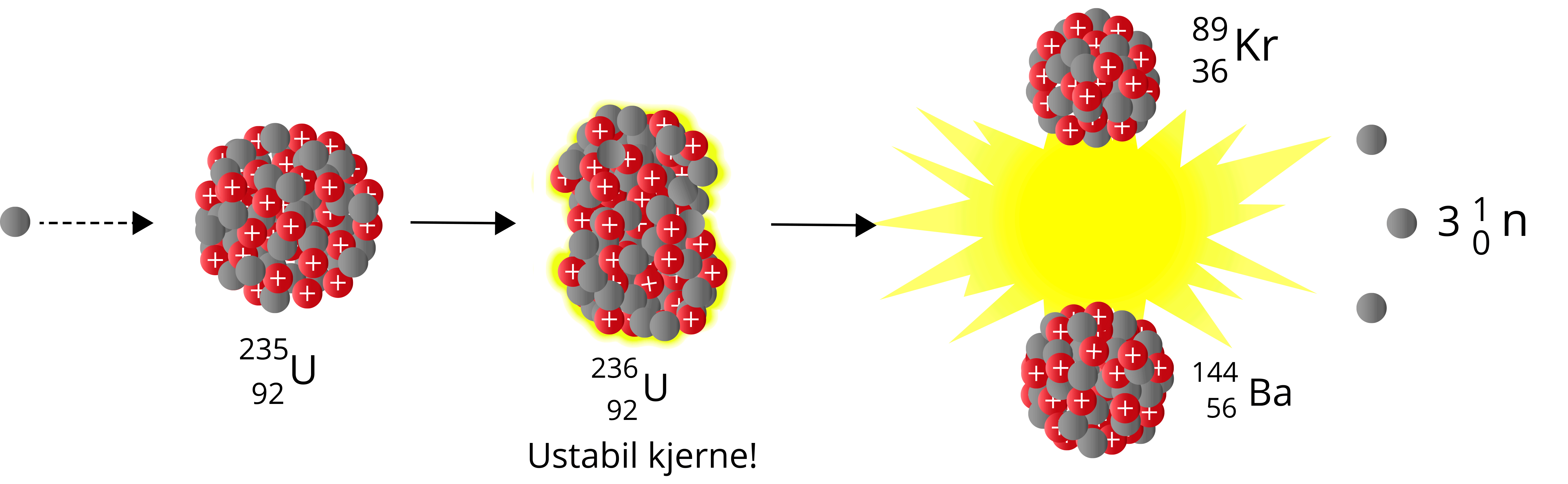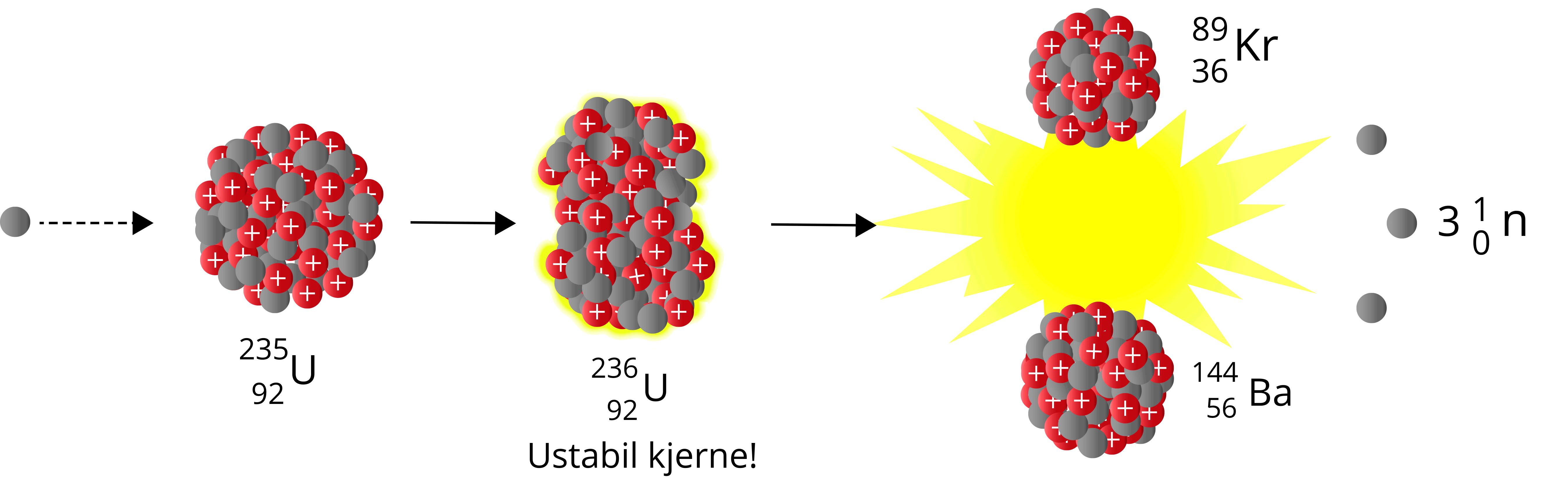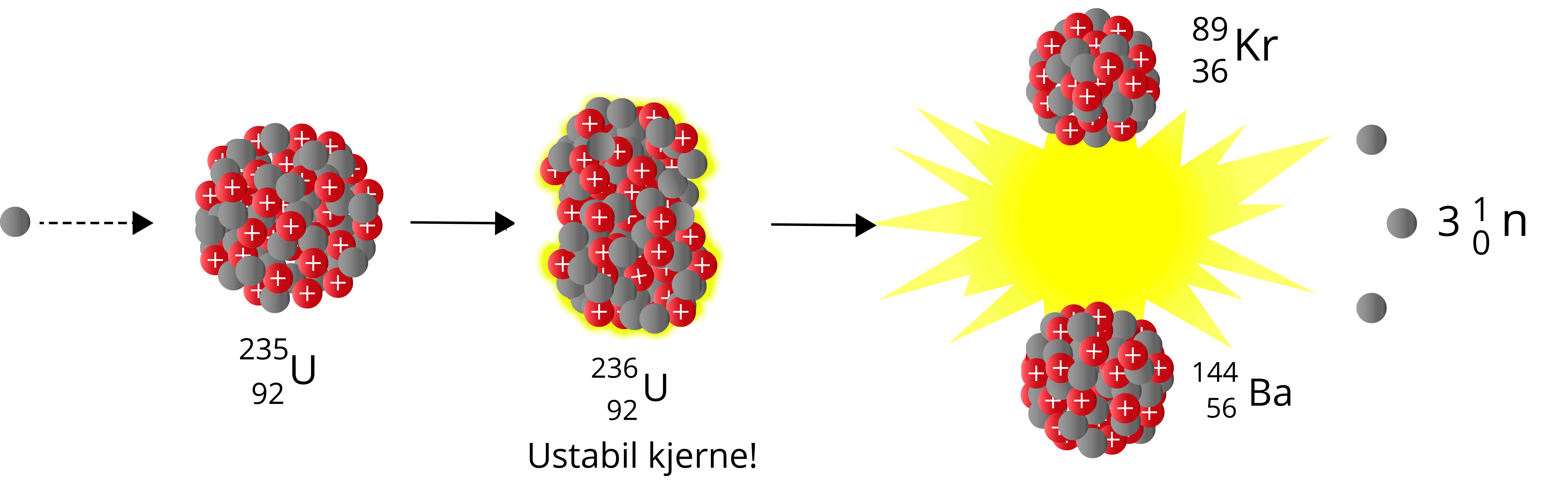
\({^{1}_{0}\text{n}} + {^{235}_{\,\,92}\text{U}} \to {^{236}_{\,\,92}\text{U}} \to \,{^{89}_{36}\text{Kr}} + {^{144}_{\,\,56}\text{Ba}} + 3{^{1}_{0}\text{n}}\)
Av figur 3 ser vi at store kjerner til høyre jern kan fisjonere til 2 eller flere mindre nuklider og på denne måten få et massesvinn. Vi ser også at kjerner med lavere nukleontall enn jern kan fusjonere til én litt større kjerne og på denne måten få et massesvinn.
Massesvinnet i både fusjonen og i fisjonen vil utgjøre det vi kaller reaksjonsenergien – det er snakk om relativt store mengder bindingsenergi som frigjøres. Denne energien går for eksempel til elektromagnetisk strålingElektromagnetisk stråling er stråling i form av pakker med ren energi kalt fotoner, som sendes fra en strålingskilde. Den elektromagnetiske strålingen kan oppfattes både som bølger og partikler., eller økt kinetisk energiBevegelsesenergi: Ethvert legeme i bevegelse har bevegelsesenergi. Energimengden er bestemt av massen og farten til legemet etter formelen Ek = ½mv². for produktene, og vi beregner den ved hjelp av Einsteins formel: $$E_r = m_sc^2$$
\(m_s \) beregner vi ved hjelp av denne formelen: $$m_s = m_{\text{reaktanter}} – m_{\text{produkter}}$$
Det er denne energien vi er ute etter å utnytte i kjernekraftverk. Videre kan du lese om fusjon, bruk av thorium som brensel i kjernekraftverk, og om utfordringene ved kjernekraft og om vanlige misforståelser dertil.

 Denne artikkelen skrevet av UngEnergi er lisensiert under en
Denne artikkelen skrevet av UngEnergi er lisensiert under en