Vi skal nå snakke mer dyptgående om elektrisitet og hvordan man kan regne med elektrisk ladning. Vi har også en introduksjonstekst  til elektrisitet, som gir grunnleggende forklaringer av hva ladning, elektrisk strøm og spenning er. Vi kommer derfor ikke til å ta for oss disse begrepene like grundig her.

 

I denne teksten bruker vi ordene elektrisitet og strøm om hverandre og sikter i alle tilfeller til elektrisk strøm. Det vil si at vi ikke kommer til å snakke om konsepter som statisk elektrisitet og lignede. Vi kommer også kun til å snakke om likestrøm.

 

Elektrisk ladning

 

Elektrisk ladning er en fundamental egenskap ved partikler som protoner, elektroner og ioner. Det finnes to typer elektrisk ladning: negativ og positiv. Like ladninger frastøter hverandre, mens ulike ladninger tiltrekker hverandre. Med større ladninger blir kraften mellom de ladde partiklene større. Enheten for elektrisk ladning er coulomb, C og ladning angis som regel med bokstaven q i formler.

Ladningen til et enkelt proton kalles elementærladningen og betegnes med en e. Verdien til elementærladningen er ca. $$  {\enspace e=1,6 \cdot 10^{-19}  {C} \enspace } $$

Dette betyr at du trenger ca. 6 300 000 000 000 000 000 protoner for at de til sammen skal ha en ladning på 1 coulomb! Et elektron har ladningen –e. Elektroner og protoner er den minste ladningen vi har. Dette betyr at ladningen til alle partikler må være et heltall ganger elementærladningen. Du kan for eksempel ikke ha en partikkel med ladning på 2,5⋅e, fordi 2,5 ikke er et heltall.

 

Rundt en elektrisk ladning ligger det vi kaller et elektrisk felt. Feltet påvirker, og påvirkes av, andre elektriske felt i nærheten. Motsatt ladde felt trekkes mot hverandre, og likt ladde felt frastøter hverandre. Denne påvirkningen kan også kalles en kraft. Denne kraften er proporsjonal med størrelsen på ladningen den virker på. Hvis ladningen er dobbelt så stor vil kraften som virker på ladningen også dobles.

 

 

Spenning

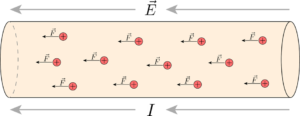
Når man kobler et batteri til en krets, får man en positiv og en negativ pol i hver sin ende av kretsen. Mellom disse polene oppstår det et elektrisk felt gjennom hele kretsen fra positiv til negativ pol. Feltet vil dytte på alle de løse ledningselektroner i kretsen, slik at de starter å bevege seg i samme retning. Det elektriske feltet mellom polene er derfor grunnen til at vi får en strøm i kretsen.

 

Når man skal beskrive strømmen i en ledning er det lettere å se på potensiell energi enn å studere feltstyrke. Et elektron i starten av en krets har høyere potensiell energi enn et i slutten av kretsen. Å flytte et elektron fra et punkt med lav potensiell energi, til et punkt med høyere potensiell energi, krever et arbeid. Dette er på samme måte som en stein har høyere potensiell energi øverst i en bakke enn nederst, og det krever arbeid for å flytte den opp bakken.

 

Vi ser nå på et punkt A i starten av kretsen, og et punkt B mot slutten av kretsen. Å flytte et elektron fra B til A, krever et arbeid på grunn av forskjellen i potensiell energi. Derfor vil den samme forflytningen i motsatt retning, altså fra A til B, gi et negativt arbeid. $$  {\enspace W_{AB} = E_{pB} \verb@ – @ E_{pA} \enspace } $$

E_pA og E_pB er den potensielle energien til elektronet i henholdsvis A og B. W_AB er arbeidet på elektronet fra A til B. Den potensielle energien til en partikkel er proporsjonal med ladningen til partikkelen, på samme måte som kraften.

 

Arbeidet for å flytte ladningen fra A til B vil derfor avhenge av hvor mye ladning som flyttes. Ved å dele arbeidet på ladningen, q, får vi et uttrykk for arbeidet som ikke avhenger av om det er mye eller lite ladning som flyttes. $$  {\enspace U_{AB} = \frac{W_{AB}}{q}\enspace } $$

Arbeid per ladning er definisjonen på det vi kaller spenning, betegnet med en U. Her betyr U_AB spenningen mellom punktene A og B. Spenning måles i størrelsen volt, V. Om du ser for deg elektrisitet som vann som strømmer i en slange, så vil spenning være pumpen som sørger for trykket som dytter vannet rundt i slangen. Senere skal vi komme tilbake til hvordan man regner med spenning, men først må vi snakke litt om elektrisk strøm.

 

Elektrisk strøm

Elektrisk strøm er definert som ladning i bevegelse. I vårt tilfelle er dette elektroner som beveger seg gjennom metaller. Strøm betegnes vanligvis med symbolet I og måles i Ampere, A. Hvor stor strømmen er sier noe om hvor mye ladning som passerer et tverrsnitt av en ledning i løpet av et sekund. For å forstå dette kan du se for deg at du står på kanten av en enveiskjørt vei og teller hvor mange biler som kjører forbi i løpet av ett minutt. Her er veien ledningen vår, og vi teller i stedet antall elektroner som passerer et tverrsnitt av ledningen i løpet av et sekund.

 

For å finne mengden ladning, q, som har passert tverrsnittet i steder for antall elektroner, ganger vi antall elektroner med ladningen til et elektron. $$  {\enspace q = antall \verb@ @ elektroner \cdot -e  \enspace } $$

Dersom vi måler mengden ladning over lengre tid, må vi også dele på hvor mange sekunder vi målte. Dermed får vi følgende formel $$  {\enspace I = \frac{q}{t}\enspace } $$ der t er symbolet for tid. Altså blir 1 Ampere = 1 Coulomb / 1 sekund.

 

Sammenhengen mellom spenning og strøm

Et naturlig spørsmål å stille nå er om det finnes en fin sammenheng mellom spenning og strøm. Vil økt spenning bety at strømmen også øker? I de aller fleste tilfeller stemmer dette. Hvor mye strømmen øker med er en helt annen sak. For å kunne studere dette definerer vi resistansen, R, som forholdet mellom spenningen og strømmen: $$  {\enspace R = \frac{U}{I}\enspace } $$

Resistansen har enheten ohm, Ω. Som du kanskje skjønner ut ifra navnet sier resistansen noe om hvor mye motstand (på engelsk: resistance) elektronene møter på sin ferd gjennom ledningen. Hvordan resistans faktisk fungerer er veldig komplisert, men man kan se for seg følgende modell for å forstå konseptet bedre: når elektronene beveger seg fremover i metallet må de passere mange atomkjerner. Underveis vil de kollidere med mange av disse, noe som gjør at de mister fart og dermed ikke klarer å bevege seg spesielt fort fremover. Se for deg at du prøve å bevege deg raskt gjennom en stor folkemengde: det er kronglete og du møter mye motstand når du prøver å dytte deg fram.

 

For de fleste gode ledere er resistansen relativt konstant. Den øker derfor ikke betydelig ved økt spenning. Dermed blir forholdet mellom spenning og strøm tilnærmet proporsjonalt. Det vil si at spenningen er lik strømmen ganger en konstant. Dette spesialtilfellet er så viktig at det har fått sitt eget navn: $$\boxed{\textbf{Ohms lov:} \\ \begin{equation} U = R\cdot I \end{equation},\: der\:R\: er\: konstant \enspace} $$

Hvis man da kjenner resistansen vil man alltid kjenne forholdet mellom strømmen og spenningen, noe som er veldig greit å regne med.

 

Regning med strøm og spenning

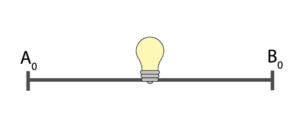
I virkeligheten har alle ledninger en viss motstand, men i de fleste utregninger på videregående ser man bort fra denne motstanden. Vi kommer derfor til å gjøre det samme her. Om vi ser på et ledningsstykke uten komponenter, vil forskjellen i potensiell energi mellom to punkter A₀ og B₀ på ledningsstykket være 0. Det er derfor egentlig bare relevant å diskutere spenningen mellom punkter som har en komponent med resistans mellom seg.

 

En komponent som kun har resistans og ikke fungerer til noe annet kalles en motstand. Denne fungerer som en flaskehals, som senker strømhastighet. Andre komponenter som lyspærer og brytere har også resistans, men har i tillegg et annet formål i kretsen.

 

Med dette i bakhodet skal vi nå se på noen typer kretser.

 

Elektrisk strøm i seriekobling

 

En seriekobling er en krets der komponentene kobles etter hverandre i en ring, se figuren over. Over batteriet står det at spenningen over hele kretsen er 12 V, og vi kan også se at alle motstandene til sammen gir en total resistans i kretsen på 8 Ω. Vi kan dermed bruke Ohms lov for å finne strømmen i kretsen:

$$  {U = R \cdot I} $$

$$  {\implies I = \frac{U}{R} = \frac{12 \ \Omega}{8 \ V} = 1,5  \ A }$$

I en seriekobling er strømmen lik over alt.

 

Ved hjelp av Ohms lov kan vi også regne ut spenningen over de ulike komponentene i kretsen. For eksempel vil spenningen over komponentene i figuren over bli:

$$  {1.\ \ U = R \cdot I = 3 \ \Omega \cdot 1,5  \ A = 4,5 \ V for\ lysbryteren \\ 2. \ \ U = R \cdot I = 5 \ \Omega \cdot 1,5  \ A = 7,5 \ V for\ lyspæra} $$

Spenningen over en komponent betyr egentlig bare spenningen mellom et punkt før og et punkt etter komponenten. For eksempel er spenningen over lysbryteren lik U_AB, og spenningen over lyspæra er lik U_BC.

 

Du ser kanskje at summen av spenningen over alle komponentene til sammen blir 12 V. Dette viser seg å alltid være tilfelle og er en lov oppkalt etter mannen som først beskrev dette.

 

$$\boxed{\textbf{Kirchhoffs spenningslov:} \\ \text{Summen av spenningen over alle komponenter i en krets må være lik spenningen over hele kretsen. }} $$

 

Denne loven er svært nyttig. Hvis man for eksempel ikke kjenner resistansen over en av komponentene i en krets, kan man da regne den ut ved hjelp av Kirchoffs spenningslov og Ohms lov.

 

Når strømmen passerer gjennom en komponent med resistans, mister vi noe av spenningen. Dette kalles et spenningsfall. I punktet A er spenningen 12V, siden vi ikke har hatt noe spenningsfall enda. I punktet B, etter at strømmen har gått gjennom bryteren, er spenningen 7,5V. Vi har altså hatt et spenningsfall på 4,5V.

 

Dette kan illustreres med et skjema som vist nedenfor. Kretsen er den samme som i figuren over, men tegnet på en litt annen måte.

 

Som tidligere nevnt er spenningen i batteriet det samme som spenningen over hele kretsen, men hvorfor er det sånn? Punktene A og C tilsvarer positiv og negativ pol. Dette er de to punktene som er lengst unna hverandre når man følger strømretningen, og som derfor har størst forskjell i potensiell energi. Siden batteriet er spenningskilden, så vil summen av spenningsfallet over alle komponentene i kretsen være lik spenningen som batteriet produserer. Hvis vi måler spenningen fra punkt C til punkt A, U_CA, vil vi se at den blir -12 V, fordi ladningen til elektronene   q = –e. Vi ser derfor heller på spenningen fra A til C, U_AC, som da blir 12 volt.

 

Elektrisk strøm i parallellkobling 

 

En parallellkobling er en krets med forgreininger. Det vil si at kretsen har et eller flere punkter, der flere ledninger er koblet sammen. I et slikt punkt vil strømmen ”dele” seg, litt som en elv som forgreiner seg. Akkurat som vannet, vil den elektriske strømmen ”foretrekke” den greina med minst motstand. Hvis strømledningene møtes igjen vil mengden strøm være den samme etter forgreiningen som før. Dette er enda en lov formulert av Kirchhoff:

 

$$\boxed{\textbf{Kirchhoffs strømlov:} \\ \text{Summen av all strømmen som går inn mot et forgreningspunkt er lik summen av strømmen som går ut.}} $$

 

Dette er fordi strøm ikke kan oppstå, forsvinne eller hope seg opp i et forgreningspunkt. Dermed må summen av strøm inn i et forgreningspunkt, være like strømmen ut. Av samme grunn er strømmen i en seriekobling lik over alt i kretsen.

 

Effekt

Se for deg at du og en klone av deg skal springe 60 meter. Du springer de 60 meterne på 10 sekund, mens klonen din springer dem på 12 sekunder. Dere har sprunget like langt, og har derfor gjort et like stort arbeid for å komme dere fra start til mål, selv om du sprang 2 sekunder fortere enn klonen din. Forskjellen ligger i at du var mer effektiv enn klonen din. Samtidig gjelder det også at om både du og klonen din løper i 15 sekunder, men du løper 20 meter lengre enn klonen din, har du vært mer effektiv. Effekt handler altså om hvor stort arbeid man har gjort, delt på tiden som er brukt.

 

Når vi snakker om elektrisitet, er effekten hvor effektivt elektronene flytter seg gjennom en krets. Vi kan på en måte se på det som farten til elektronene. Desto høyere effekt, desto kjappere beveger elektronene seg gjennom kretsen.

 

Definisjonen av effekt, P, er arbeid per tidsenhet. Ved å bruke sammenhengen mellom spenning og arbeidet utført på elektronene i en krets får vi:

$$  {P = \frac{W_{AB}}{t} = \frac{U_{AB} \cdot q }{t}} $$

$$  {\implies P = U_{AB} \cdot I}$$

Der vi i den siste overgangen har brukt at definisjonen på strøm er ladning per tidsenhet. Enheten for effekt er watt, W .